« Problème de Héron » : différence entre les versions
m →Références : + |
m →Extensions : ++ |
||
| Ligne 13 : | Ligne 13 : | ||
=== Problème dans le triangle === |
=== Problème dans le triangle === |
||
[[Image:Tri napoleon f21.svg|vignette|droite|upright=1.5|Construction du point de Fermat.]] |
[[Image:Tri napoleon f21.svg|vignette|droite|upright=1.5|Construction du point de Fermat.]] |
||
{{article détaillé|Point_de_Fermat#Illustration_mécanique}} |
|||
Pour trois points, le problème revient au [[Point_de_Fermat#Illustration_mécanique|problème de Fermat]] : pour un triangle ''ABC'', trouver le point ''M'' tel que ''AM''+''BM''+''CM'' soit minimale. |
|||
Il apparait que le point solution existe si aucun angle du triangle ''ABC'' n'excède 120° et c'est alors le [[point de Fermat|point de Fermat-Steiner-Torricelli]] du triangle ; si un des angles est supérieur à 120°, le point recherché est le sommet de cet angle. |
Il apparait que le point solution existe si aucun angle du triangle ''ABC'' n'excède 120° et c'est alors le [[point de Fermat|point de Fermat-Steiner-Torricelli]] du triangle ; si un des angles est supérieur à 120°, le point recherché est le sommet de cet angle. |
||
{{clr}} |
{{clr}} |
||
=== Problème avec ''n'' points === |
|||
{{article détaillé|Problème de Weber}} |
|||
Au début du {{s-|XX}}, l'économiste allemand [[Alfred Weber]] s'intéresse au cas général de la minimalisation pour un problème à ''n'' points. |
|||
=== Extension dans l'espace : le problème de Gergonne === |
=== Extension dans l'espace : le problème de Gergonne === |
||
| Ligne 23 : | Ligne 28 : | ||
Le problème de Gergonne s'énoncé ainsi : pour un plan (''P'') et trois points ''A'', ''B'', ''C'' non alignés et non situés sur (''P''), trouver le point ''M'' sur (''P'') tel que ''AM''+''BM''+''CM'' soit minimale<ref>{{article |lang=en |titre=The Gergonne problem |auteur=Nikolaos Dergiades |lire en ligne=https://forumgeom.fau.edu/FG2001volume1/FG200111.pdf |périodique=Forum Geometricorum |volume=1 |année=2001 |pages={{p.|75–79}} |ISSN=1534-1178}}</ref>. |
Le problème de Gergonne s'énoncé ainsi : pour un plan (''P'') et trois points ''A'', ''B'', ''C'' non alignés et non situés sur (''P''), trouver le point ''M'' sur (''P'') tel que ''AM''+''BM''+''CM'' soit minimale<ref>{{article |lang=en |titre=The Gergonne problem |auteur=Nikolaos Dergiades |lire en ligne=https://forumgeom.fau.edu/FG2001volume1/FG200111.pdf |périodique=Forum Geometricorum |volume=1 |année=2001 |pages={{p.|75–79}} |ISSN=1534-1178}}</ref>. |
||
{{clr}} |
{{clr}} |
||
=== Généralisation === |
|||
D'autres études ont été menées sur des cas où les distances ne sont pas calculées entre points mais entre espaces convexes<ref>{{article |lang=en |titre=A Look at the Generalized Heron Problem through the Lens of Majorization-Minimization |auteur1=Eric C. Chi |auteur2=Kenneth Lange |périodique=Am Math Mon |date=février 2014 |volume=121 |numéro=2 |pages=95-108 |doi=10.4169/amer.math.monthly.121.02.095#sthash.QTTb5Z6T.dpuf |lire en ligne=https://arxiv.org/pdf/1203.0578}}. |
|||
</ref>. |
|||
== Voir aussi == |
== Voir aussi == |
||
Dernière version du 2 mai 2024 à 15:40
Cet article est une ébauche concernant la géométrie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
En géométrie, le problème de Héron est un problème d'optimisation qui consiste à trouver le plus court chemin entre deux points après un contact avec une droite. Il est nommé d'après Héron d'Alexandrie.
Énoncé du problème[modifier | modifier le code]
Le problème de Héron est un problème connu : avec une droite (d) et deux points A et B ne se trouvant pas sur (d), placer un point M sur (d) tel que AM + MB soit minimale.
Ce problème peut se résoudre avec les outils de l'optimisation, cependant un raisonnement purement géométrique donne un résultat plus simple et plus lisible : pour trouver le point solution M, il suffit de construire le symétrique A' de A par rapport à (d), puis de marquer M comme l'intersection de A'B et (d). En effet, par le principe de Fermat, le chemin le plus court dans le plan euclidien étant la ligne droite, on trace ainsi la ligne brisée la plus courte[1].
Extensions[modifier | modifier le code]
Problème dans le triangle[modifier | modifier le code]
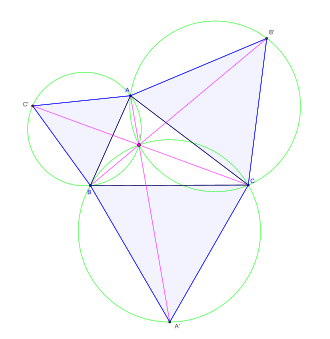
Pour trois points, le problème revient au problème de Fermat : pour un triangle ABC, trouver le point M tel que AM+BM+CM soit minimale.
Il apparait que le point solution existe si aucun angle du triangle ABC n'excède 120° et c'est alors le point de Fermat-Steiner-Torricelli du triangle ; si un des angles est supérieur à 120°, le point recherché est le sommet de cet angle.
Problème avec n points[modifier | modifier le code]
Au début du XXe siècle, l'économiste allemand Alfred Weber s'intéresse au cas général de la minimalisation pour un problème à n points.
Extension dans l'espace : le problème de Gergonne[modifier | modifier le code]
Le problème de Gergonne s'énoncé ainsi : pour un plan (P) et trois points A, B, C non alignés et non situés sur (P), trouver le point M sur (P) tel que AM+BM+CM soit minimale[2].
Généralisation[modifier | modifier le code]
D'autres études ont été menées sur des cas où les distances ne sont pas calculées entre points mais entre espaces convexes[3].
Voir aussi[modifier | modifier le code]
Références[modifier | modifier le code]
- François Rouvière, « Histoires de maxima et minima », Séminaire "Enseignement des Mathématiques", (lire en ligne).
- (en) Nikolaos Dergiades, « The Gergonne problem », Forum Geometricorum, vol. 1, , p. 75–79 (ISSN 1534-1178, lire en ligne)
- (en) Eric C. Chi et Kenneth Lange, « A Look at the Generalized Heron Problem through the Lens of Majorization-Minimization », Am Math Mon, vol. 121, no 2, , p. 95-108 (DOI 10.4169/amer.math.monthly.121.02.095#sthash.QTTb5Z6T.dpuf, lire en ligne).
