« Cercles d'Apollonius » : différence entre les versions

Navigation interactive dans l’historique

Contenu supprimé Contenu ajouté

Intégrés

Dernière version du 27 avril 2024 à 18:09

En géométrie, le nom de cercles d'Apollonius a été donné à plusieurs configurations différentes.

Cercles d'Apollonius associés à deux points[modifier | modifier le code]

Apollonius de Perge propose de définir le cercle comme l'ensemble des points M du plan pour lesquels le rapport des distances MA/MB reste constant, les points A et B étant donnés.

Définition — Si A et B sont deux points distincts et k est un réel strictement positif différent de 1, le cercle d'Apollonius relativement aux points A et B et de rapport k est l'ensemble des points M du plan tels que

{\frac {MA}{MB}}=k.

Démonstration du fait que ce lieu géométrique est bien un cercle, et construction de ce cercle :

Solution sur (AB) : si k = 1, MA=k MB a une unique solution sur (AB) : le milieu de [AB]. Sinon le problème d'Apollonius MA = k MB a deux solutions sur (AB), disons C et son conjugué harmonique D par rapport à A et B ; D existe dès que C n'est pas le milieu de [AB].
Solution hors de (AB) : Si MA/MB = k, alors MA/MB = CA/CB ; (MC) est alors la bissectrice de l'angle en M dans le triangle AMB. Mais on a aussi MA/MB = DA/DB et (MD) est la seconde bissectrice de l'angle en M dans AMB. En particulier le triangle CMD est rectangle en M et M est donc sur le cercle de diamètre [CD].
Synthèse : Pour tout M du plan hors de (AB) les droites (MA), (MB), (MC) et (MD) forment un faisceau harmonique. Si de plus M est sur le cercle de diamètre [CD], on sait alors que (MC) et (MD) sont les bissectrices intérieures et extérieures en M du triangle AMB. On conclut avec la caractérisation de la bissectrice en termes de rapport.
Le cercle de diamètre [CD] est le cercle d'Apollonius relativement aux points A et B et de rapport k.

On peut aussi remarquer que ce lieu est obtenu par l'annulation de la fonction scalaire de Leibniz $MA^{2}-k^{2}MB^{2}$ ; si $G$ est le barycentre de $A(1)$ et $B(-k^{2})$ , le lieu est le cercle de centre $G$ et de rayon ${\frac {k}{|k^{2}-1|}}AB$ .

Pour k variant, ces cercles forment un faisceau de cercles à points limites A et B.

Faisceau de cercles d'Apollonius d'un triangle[modifier | modifier le code]

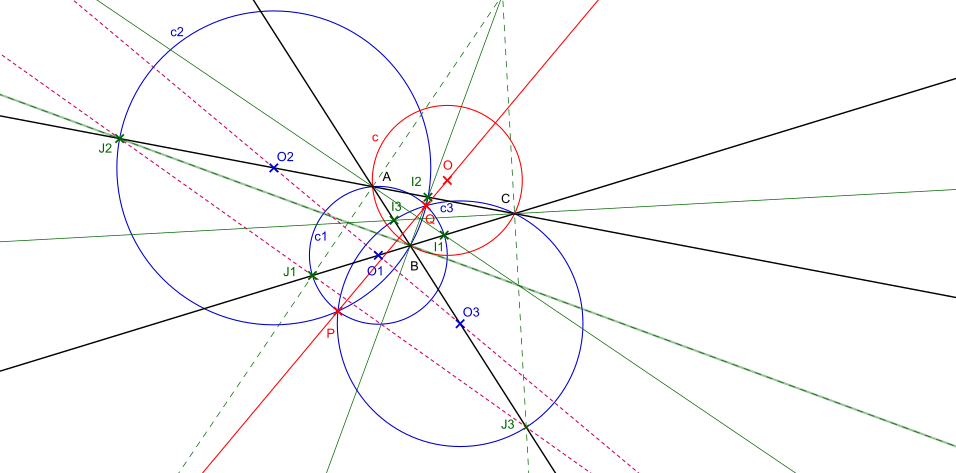
Soit ABC un triangle. Le cercle c de centre O est circonscrit au triangle ABC.

Les bissectrices en A coupent [BC] en I₁ et J₁, le cercle c₁ de centre O₁ a pour diamètre [I₁J₁].

Les bissectrices en B coupent [AC] en I₂ et J₂, le cercle c₂ de centre O₂ a pour diamètre [I₂J₂].

Les bissectrices en C coupent [AB] en I₃ et J₃, le cercle c₃ de centre O₃ a pour diamètre [I₃J₃].

Le faisceau de cercles d'Apollonius est formé par les trois cercles c₁, c₂ et c₃ d'Apollonius qui ont en commun les deux points P et Q. Ce sont les points de base du faisceau.

Leurs centres O₁, O₂ et O₃ sont alignés sur la médiatrice de [PQ].

Le centre O du cercle circonscrit c et le point de Lemoine du triangle ABC sont situés sur la droite (PQ).

Les points Q (X15) et P (X16) sont les points isodynamiques du triangle ABC. Ce sont les conjugués isogonaux des points de Fermat (X14 et X13)

Cercles d'Apollonius associés à trois cercles donnés[modifier | modifier le code]

Le problème d'Apollonius, ou problème des contacts consiste à déterminer les cercles tangents à trois cercles donnés. En partant de trois cercles tangents deux à deux, et en itérant, on obtient une figure fracatale ; voir : Cercles d'Apollonius (fractale).

Bibliographie[modifier | modifier le code]

Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, (ISBN 978-2-91-635208-4)
Méthodes modernes en géométrie de Jean Fresnel
Bruno Ingrao, Coniques affines, euclidiennes et projectives, C&M, (ISBN 978-2-916352-12-1)

Portail de la géométrie

@@ Ligne 1 : / Ligne 1 : @@
-En géométrie, le nom de '''cercles d'[[Apollonius de Perga|Apollonius]]''' a été donné à plusieurs configurations différentes.
+{{Confusion|Cercles d'Apollonius (fractale)}}
+En géométrie, le nom de '''cercles d'[[Apollonios de Perga|Apollonius]]''' a été donné à plusieurs configurations différentes.
 == Cercles d'Apollonius associés à deux points ==
-[[Apollonius de Perga|Apollonius de Perge]] propose de définir le cercle comme l'ensemble des points ''M'' du plan pour lesquels le rapport des distances ''MA''/''MB'' reste constant, les points ''A'' et ''B'' étant donnés.
+[[Apollonios de Perga|Apollonius de Perge]] propose de définir le cercle comme l'ensemble des points ''M'' du plan pour lesquels le rapport des distances ''MA''/''MB'' reste constant, les points ''A'' et ''B'' étant donnés.
 {{théorème|1=
 |style=display:table;|énoncé=Si ''A'' et ''B'' sont deux points distincts et ''k'' est un réel strictement positif différent de 1, le cercle d'Apollonius relativement aux points ''A'' et ''B'' et de rapport ''k'' est l'ensemble des points ''M'' du plan tels que

v · m Triangles
Description	Sommet Apex Côté Angle Base
Types	Triangle équilatéral Triangle isocèle Triangle d'or Triangle rectangle Angle droit Cathète Hypoténuse Triangle de Kepler Triangle obtusangle Triangle acutangle Triangle isocèle rectangle Triangle pseudo-rectangle Triangle scalène Triangle de Héron
Points remarquables (Nombre de Kimberling)	Centres : Centre du cercle inscrit Centre de gravité Centre du cercle circonscrit Orthocentre Centre du cercle d'Euler Centre du cercle de Spieker Points de Brocard Points de Feuerbach Point de Fermat ou Point de Torricelli Point de Longchamps Point de Miquel Point de Gergonne Point de Nagel Point de Vecten Points isogonaux Points isodynamiques Point de Lemoine Points de Terquem Points de Napoléon Mittenpunkt
Droites remarquables	Cévienne Hauteur Médiane Bissectrice Médiatrice Droite de Brocard Droite d'Euler Droite de Lemoine Droite de Newton Droite de Simson (ou droite de Wallace) Droite de Steiner Ménélienne Symédiane Axe orthique Droite centrale
Cercles remarquables	Cercle circonscrit Cercle exinscrit Cercle inscrit Cercle d'Euler Cercle d'Apollonius Cercles de Lemoine Cercle de Longchamps Cercle de Miquel Cercle de Taylor Cercle de Tucker Cercle podaire Cercle de Brocard Cercle de Spieker Cercle de Fuhrmann Cercles de Johnson Cercle pédal
Triangles remarquables	Triangle de Bevan Triangle de Feuerbach Triangle de Gergonne Triangle de Morley Triangle de Nagel Triangle inscrit de périmètre minimal (Problème de Fagnano) Triangle médian Triangle orthique Triangle podaire Triangle tangentiel Triangle de Fuhrmann
Courbes remarquables	Deltoïde de Steiner Coniques Conique inscrite de Serret (ou de MacBeath) Conique orthique Hyperbole de Kiepert Paraboles Parabole tritangente Parabole de Kiepert Ellipses Ellipse de Mandart Ellipse de Steiner Coniques circonscrites et inscrites à un triangle Cubiques
Théorèmes	Théorème de Pythagore Théorème de Thalès Théorème de Napoléon Théorème japonais de Carnot Théorème de Ménélaüs Théorème de Morley Théorème de Nagel Théorème de Neuberg Théorème de Hamilton Théorème d'Euler Théorème de Feuerbach Théorème de Viviani Avec des céviennes Théorème de Ceva Théorème de Gergonne Théorème de Stewart Théorème de Terquem Théorème de Routh Théorème de Jacobi Avec des cercles Théorème des six cercles Théorème des trois cercles de Miquel
Relations entre triangles	Triangles isométriques Triangles semblables Inégalités dans le triangle
Résolution	Loi des cosinus Loi des sinus Loi des tangentes Loi des cotangentes Aire Formule de Héron